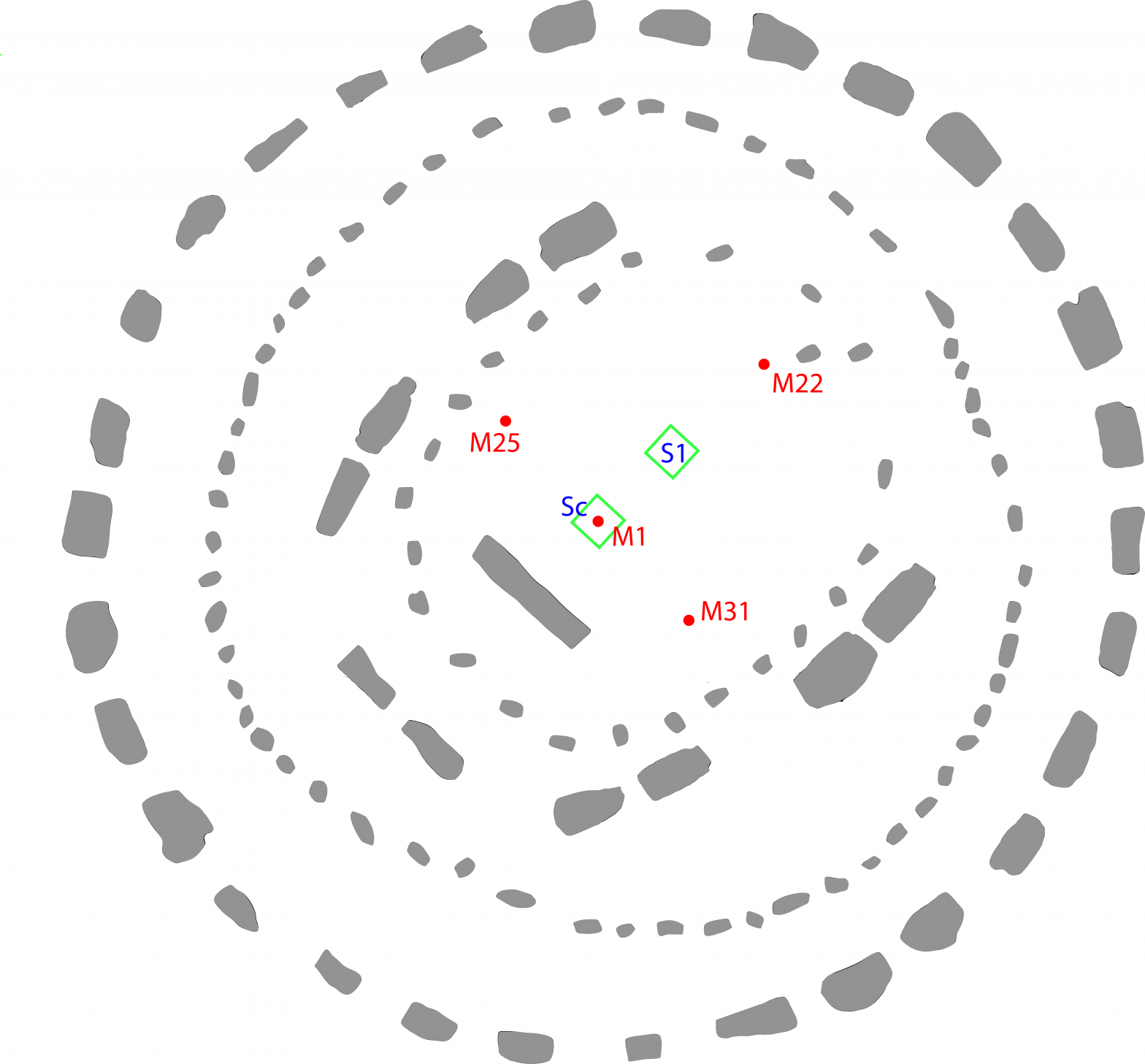
Early Decay Time, EDT
In a previous blog I wrote about the Reverberation Time within Stonehenge based on our acoustic scale model of the 2200 BC configuration. While the reverberation time is very commonly used to characterise rooms, it’s not the best metric in all circumstances. The reverberation time is how long it takes sound to decay by 60 dB, but when listening to on-going music, you might not hear that full decay because new notes come along too quickly and drown out the old ones. Consequently, a better measure for perceived reverberance (in concert halls) is the Early Decay Time (EDT), which is evaluated over the first 10 dB of decay [1].
To get a rough sense of the EDT in Stonehenge, Figure 1 shows an average over all positions. But averages in EDT should be treated with caution. As the metric is calculated over early parts of the sound decay, it’s highly influenced by the presence (or not) of reflections from stones close to the source or listener. The EDT varies greatly with position in Stonehenge, as shown by the large standard deviations (the error bars) [2].
How EDT various in Stonehenge
Line of Sight

Back in 2,200 BC it is thought there were 157 stones. As the photo above shows, there would have been many places where a listener would not be able to see a talker due to obscuring stones. You would still have been able to hear the talker via sound reflecting from, or bending around, the stones. But the sound travelling direct from talker to listener would have been greatly reduced. This has a significant effect on EDT.
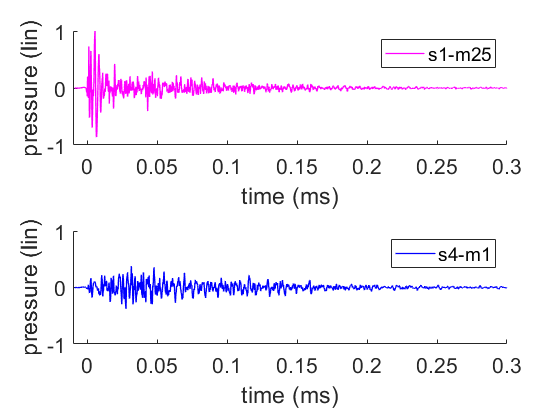
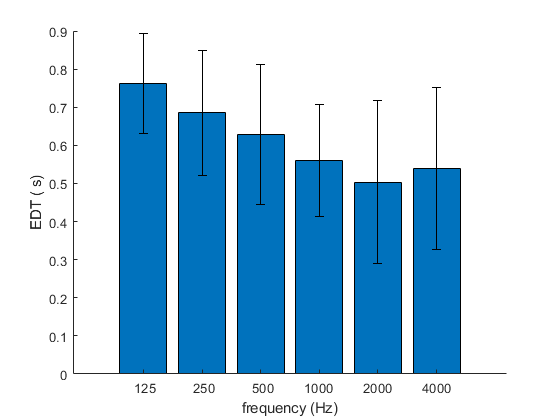
Figure 3 shows two impulse responses and Figure 4 the locations of the loudspeakers and microphones for the two measurements. For s1-m25 (top) there is a direct line of sight and the biggest sound arrives first travelling straight from source to receiver. In contrast, the trilithon in front of source s4 meant the sound couldn’t directly reach microphone m1. For s4-m1 (bottom of Figure 3) the direct sound is largely missing. The largest sounds to reach this occluded microphone comes from reflections.
The EDT for the case where there was a clear line of sight between loudspeaker and microphone (s1-m25) is about 0.4s at mid-frequency. For the occluded case (s4-m1) it’s 0.8 s. The EDT is strongly affected because it’s measuring the decay of sound at the start of the impulse response.
Quantifying the effect of occlusion on EDT
Each of the thirty measurements was classified into three categories – clear line of sight, partly occluded and fully occluded – based on the loudspeaker and microphone positions. The mean mid-frequency EDT (average of 500, 1000 and 2000 Hz) for the clear and occluded cases were: [4]
- Clear line of sight, EDT = 0.55 ± 0.06
- Fully Occluded, EDT = 0.67 ± 0.08
A t-test comparing those with a clear line of sight to those fully occluded just showed a significant difference (p=0.04, Hedges’ g=1.0, large effect). A difference of 0.12s in EDT is audible.
Clustering
The next approach to make sense of the data was to do a cluster analysis. The measurements were grouped together according to which ones had similar reverberation times and EDT [5]. Figure 5 shows the average reverberation time (RT) and EDT for each of the clusters. What differentiates the clusters is the EDT, the reverberation time doesn’t vary much for the different measurements.
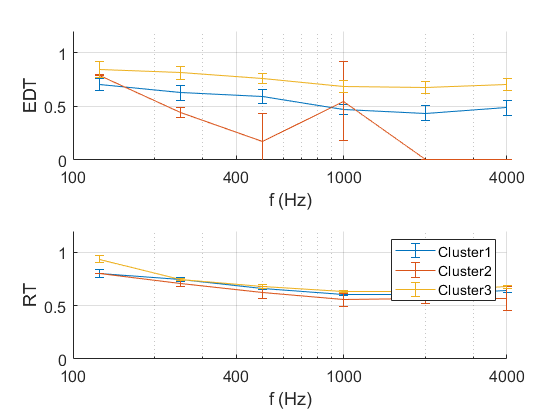
Cluster 3 (yellow) has the highest EDT and tends to have more occluded positions than the other two clusters (confirming the line of sight analysis above [6]). Cluster 2 (red) has only two measurements, and they’re all when the source and receiver are in the inner-most part of Stonehenge.
The top plot of Figure 6 shows an impulse response for one measurement from Cluster 2 (s1-m1) with a short EDT. The bottom plot is for another position in the inner part of the henge (sc-m22) but it’s in Cluster 1 and has a longer EDT. The positions of the sources and microphones are shown in Figure 7.
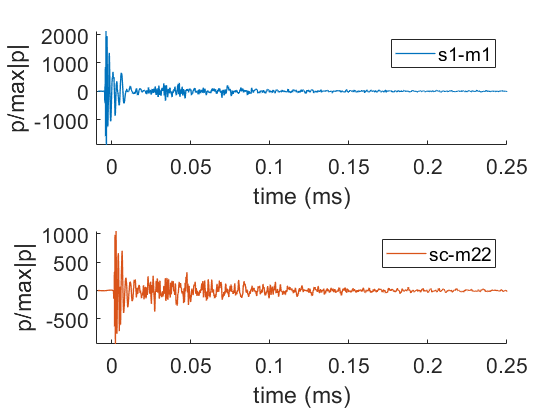
The top impulse response in Figure 6 is dominated by the sound direct from the source to the microphone, and reflections are relatively weak. This leads to the very short EDT value for s1-m1. In contrast the other case (bottom of Figure 6) has a weaker direct sound due to the source-microphone distance being longer, making the reflections more important leading to a longer EDT.
Digital Stonehenge
Figure 8 shows the EDT for the 1:12 acoustic scale model and a computer prediction by Till using a geometric room acoustic simulation (‘Digital Stonehenge’) [7]. While the lower plot shows some correspondence between the measurement and Digital Stonehenge at low-mid frequencies, there is a large divergence at high frequency. Also, the top graphs are very different. At mid-frequency in the top plot, Digital Stonehenge is giving an EDT like a medium-sized concert hall (>1s), whereas the acoustic scale model is giving a very short EDT typical of a dead studio.

The very large EDT values at the centre of Digital Stonehenge look wrong. I suspect the problem is caused by a strong floor reflection in the model, or a badly-modelled reflection from the altar stone or inner trilithons. In my next blog on echoes, I look at the impulse response for Digital Stonehenge in more detail. Digital Stonehenge is producing inaccurate results and giving a wrong impression for what the acoustics in 2,200 BC would have been like.
The 1000 Hz peak in the s1-m1 physical scale model measurements (Figure 8) look a little odd at first. But these are down to a problem with the standard way EDT is calculated when decay curves are very non-linear. (An explanation is at the bottom of the blog for those interested.)
Summary
The Early Decay Time (EDT) relates to how reverberant a place appears to a listener. It varies around Stonehenge, with a weak dependency on whether there is a line of sight between source and listener. A significant factor not tested in the blog is the role of close-by stones providing reinforcing reflections, which is highly dependent on the geometry.
The largest mid-frequency EDT is 0.86 seconds This is what you get in a medium-sized theatre used for speech drama. But two-thirds of positions in Stonehenge are significantly less reverberant, being more like a dead TV studio. Right in the centre of Stonehenge, the EDT is very short, because reflections from the stones arrive too late. Do these create an echo? I’ll look into that in another blog.
References and notes
The plots and cluster statistics page were updated 13/3/20 after correcting my code to make the octave band filtering consistent with ISO 3382 – this made a small difference to EDT values. I changed the stats model for quantifying the effects of occlusion, and reworded to make it clear that the occlusion effect was significant but small. I also simplified the discussion of problems with ‘Digital Stonehenge’. And appended a discussion about issues with EDT and non-linear decays (see bottom of blog). 16/3/20 The t-test was redone because I had a repeat measurement in the dataset.
[1] Kuttruff, H., 2016. Room acoustics. Crc Press. pp. 179. EDT also correlates well with perceived reverberance in smaller rooms, see Kaplanis, N., Bech, S., Lokki, T., van Waterschoot, T. and Holdt Jensen, S., 2019. Perception and preference of reverberation in small listening rooms for multi-loudspeaker reproduction. The Journal of the Acoustical Society of America, 146(5), pp.3562-3576. Although reverberation time and early decay time are highly correlated in the rooms tested in this paper.
[2] The average EDT is significantly smaller than the average reverberation time for 1000, 2000 and 4000 Hz. For each octave band the EDT is about 0.1s smaller.
[3] The time of flight for the direct path has been set the same in both impulse responses. These are for 125Hz – 4kHz octave bands.
[4] The partly occluded ones were removed from this analysis because the exact effect of partial-occlusion will vary considerably depending on the size of the stones in the way.
[5] k-means clustering was used. Three clusters were used because it gave clear differentiation between the groups.
[6] Chi-square test comparing number of occluded and clear line of sight measurements in clusters 1 & 3 (chi-square = 4.96, p=0.026).
[7] Till, R., 2009. Songs of the stones: the acoustics of Stonehenge. The sounds of Stonehenge, pp.17-39.
[8] Fazenda, B.M., 2013. The acoustics of Stonehenge. Acoustics Bulletin, 38(1), pp.32-37.
Why the EDT is large for 1000 Hz in Figure 8
A short summary of this, is that using EDT when the source and receiver are <3m apart in a large space is a bit daft. But I wanted to include it to illustrate the issues with Digital Stonehenge. Here is an explanation readers who are specialists in room acoustics. The EDT is calculated from 0 dB to -10 dB of the decay curve (Figure 10, decay curves are the top row). At about 0.01 s there is a reflection that comes from the floor (see impulse responses on bottom row).
- 2000 Hz (right column). The floor reflection is relatively quiet and so the 0 to -10 dB decay region is just the direct sound with no reflections and so the EDT is very short (0.006 s).
- 1000 Hz (left column). The floor reflection is louder and dramatically slows the decay so it reachers -10 dB much later. The EDT is much longer (0.7 s).
The difference in the reflection level between 1000 Hz and 2000 Hz is because the tweeter gets more directional as the frequency increases.

I wouldn’t expect this difference in EDT values to reflect what people would hear. I would expect the reverberance to be similar at 1000 Hz and 2000 Hz. The dramatic change in EDT values between the two frequencies is due to the choice of -10dB as the calculation limit.
Follow me